R 回归分析

发表于 | 更新于 | 分类于

逐步回归

逐步回归分析是以AIC信息统计量为准则，通过选择最小的AIC信息统计量，来达到删除或增加变量的目的。

AIC : 赤池信息准则(Akaike Information Criterion) ,k是模型中估计参数的数量。L是模型的似然函数的最大值。

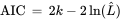
AICc：当样本量很小时，AIC很可能会选择具有太多参数的模型，即AIC会过度拟合。为了解决这种潜在的过度拟合问题，AICc可以对小样本进行校正。其中n表示样本大小，k表示参数的数量。

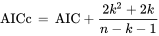
向前逐步回归

首先模型中只有一个单独解释因变量变异最大的自变量，之后尝试将加入另一自变量，看加入后整个模型所能解释的因变量变异是否显著增加（这里需要进行检验，可以用 F-test， t-test 等等）。这一过程反复迭代，直到没有自变量再符合加入模型的条件。

MASS包中的stepAIC()函数给予AIC准则实现了逐步回归模型（向前、向后和双向）。 

1
2
3
> library(MASS)
> fit <- lm(xx ~ x+y+z,data=datas)
> stepAIC(fit, direction="forward")

向后逐步回归

向后逐步回归与向前逐步回归相反，此时，所有变量均放入模型，之后尝试将其中一个自变量从模型中剔除，看整个模型解释因变量的变异是否有显著变化，之后将使解释量减少最少的变量剔除；此过程不断迭代，直到没有自变量符合剔除的条件。

1
2
3
> library(MASS)
> fit <- lm(xx ~ x+y+z,data=datas)
> stepAIC(fit, direction="backward")

向前向后逐步回归

向前向后逐步回归，这种方法相当于将前两种结合起来。可以想象，如果采用第一种方法，每加入一个自变量，可能会使已存在于模型中的变量单独对因变量的解释度减小，当其的作用很小（不显著）时，则可将其从模型中剔除。而第三种方法就做了这么一件事，不是一味的增加变量，而是增加一个后，对整个模型中的所有变量进行检验，剔除作用不显著的变量。最终尽可能得到一个最优的变量组合。

1
2
3
> library(MASS)
> fit <- lm(xx ~ x+y+z,data=datas)
> stepAIC(fit, direction="both")

Forward、Backward、Stepwise的侧重点有所不同，三种方法的选择取决于你的研究目的，如果是进行预测，在预测效果差不多的情况下，一般选择自变量最少的方法。当自变量间不存在多重共线性时，三种方法的计算结果基本一致。当自变量间存在多重共线性时，Forward侧重于引入单独作用较强的变量，Backward侧重于引入联合作用较强的变量，Stepwise介于两者之间。

全子集回归

全子集回归克服了逐步回归的缺点，即所有可能的模型都会被检验，评判准则可以是R平方、修正R平方、BIC或者Mallows Cp统计量。

R平方：

修正R平方 :

我们知道在其他变量不变的情况下，引入新的变量，总能提高模型的R2。修正R2就是相当于给变量的个数加惩罚项。换句话说，如果两个模型，样本数一样，R2一样，那么从修正R2的角度看，使用变量个数少的那个模型更优。其中n是样本数量，p是模型中变量的个数。 当p/n值很小时，如小于0.05，修正R平方将失去修正作用。

BIC：贝叶斯信息准则 ，BIC的惩罚项比AIC的大，考虑了样本数量，样本数量过多时，可有效防止模型精度过高造成的模型复杂度过高。

Mallows Cp：马洛斯的Cp值 与AIC等效。

以下为R中ISLR包的Hitters数据集为例，构建棒球运动员的多元线性模型 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
> library(ISLR)
> library(leaps)  #使用leaps做全子集回归
> Hitters <- na.omit(Hitters)
> dim(Hitters)  #除去Salary做为因变量，还剩下19个特征
[1] 263  20
> regfit.full = regsubsets(Salary~.,Hitters,nvmax = 19)  #选择最大19个特征的全子集选择模型
> reg.summary = summary(regfit.full) # 可看到不同数量下的特征选择
> plot(reg.summary$adjr2,xlab="Number of Variables",ylab="Adjusted R2",type = "l")
> points(which.max(reg.summary$adjr2),reg.summary$adjr2[11],col="red",cex=2,pch=20)  #11个特征时，Adjusted R2最大

> plot(reg.summary$cp,xlab="Number of Variables",ylab="Cp",type = "l")
> points(which.min(reg.summary$cp),reg.summary$cp[10],col="red",cex=2,pch=20) # 10个特征时，Cp最小

> plot(reg.summary$bic,xlab="Number of Variables",ylab="BIC",type = "l")
> points(which.min(reg.summary$bic),reg.summary$bic[6],col="red",cex=2,pch=20) # 6个特征时，BIC最小

> plot(regfit.full,scale = "r2") #特征越多，R2越大，这不意外，默认scale是bic。
> plot(regfit.full,scale = "adjr2")  #下图
> coef(regfit.full,11)  #查看模型的系数
 (Intercept)        AtBat         Hits        Walks       CAtBat 
 135.7512195   -2.1277482    6.9236994    5.6202755   -0.1389914 
       CRuns         CRBI       CWalks      LeagueN    DivisionW 
   1.4553310    0.7852528   -0.8228559   43.1116152 -111.1460252 
     PutOuts      Assists 
   0.2894087    0.2688277

交叉验证

交叉验证是在机器学习建立模型和验证模型参数时常用的办法，一般被用于评估一个机器学习模型的表现。更多的情况下，也用交叉验证来进行模型选择(model selection)。

k重交叉验证中，样本被分为k个子样本，轮流将k-1个子样本组合作为训练集，另外1个子样本作为测试集，这样会获得k个预测方程，记录k个测试样本的预测表现结果，然后求其平均值。测试集的目的简单来说就相当于一个游戏的内测，内部评估。进行交叉验证后得到了分数来评估你建模的准确率是高是低。最后的目的是为了哪天来了新的数据，你也可以用你的模型去预测他，相当于游戏公测。

bootstrap包中的crossval() 函数可实现k重交叉验证 ：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
> install.packages("bootstrap")  
> library(bootstrap)  
> shrinkage<-function(fit,k=10){  
  require(bootstrap)  
  theta.fit<-function(x,y){lsfit(x,y)}  
  theta.predict<-function(fit,x){cbind(1,x)%*%fit$coef}  
  x<-fit$model[,2:ncol(fit$model)]  
  y<-fit$model[,1]  
  results<-crossval(x,y,theta.fit,theta.predict,ngroup=k)  
  r2<-cor(y,fit$fitted.values)^2  
  r2cv<-cor(y,results$cv.fit)^2  
  cat("Original R-square=",r2,"n")  
  cat(k,"Fold Cross-Validated R-square=",r2cv,"n")  
  cat("Change=",r2-r2cv,"n")  
}  

> fit<-lm(Murder ~ Population+Income+Illiteracy+Frost,data=states)  
> shrinkage(fit)  
> fit2<-lm(Murder ~ Population+Illiteracy,data=states)  
> shrinkage(fit2)  
Original R-square=0.5668327
10 Fold Cross-Validated R-square=0.5193801
Change=0.04745256